前言

看，一棵二叉树！

介绍

定义

二叉树是每个节点最多有两个子树的树结构。

形态

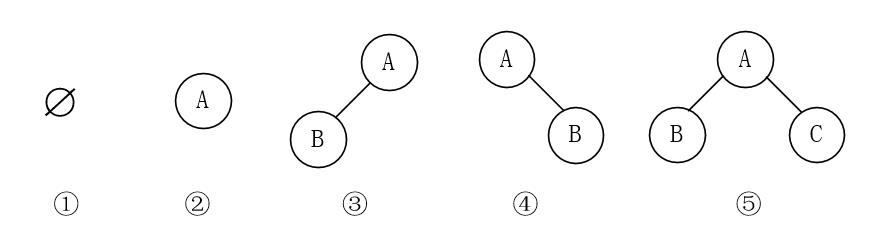
如图2-1所示，二叉树有五种形态：

节点数为0，空集
仅有一个根节点
仅有左树
仅有右树
左右树均有

满二叉树与完全二叉树

满二叉树

如果二叉树中所有分支节点的度数都为2，并且叶子节点都在通一层次上，则二叉树为满二叉树。如图2-2所示：

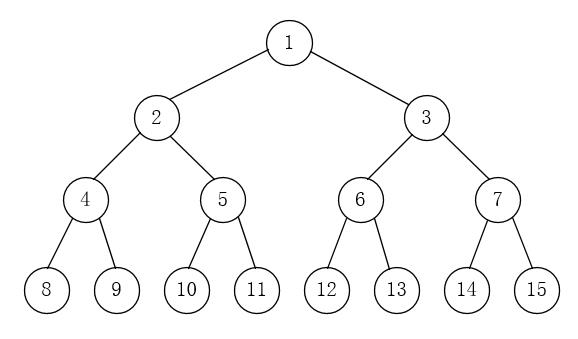
完全二叉树

对一棵具有n个节点的二叉树按层序排号，如果编号为i的节点与同样深度的满二叉树编号为i节点在二叉树中位置完全相同，就是完全二叉树。
满二叉树必须是完全二叉树，反之则不一定成立。如图2-3所示：

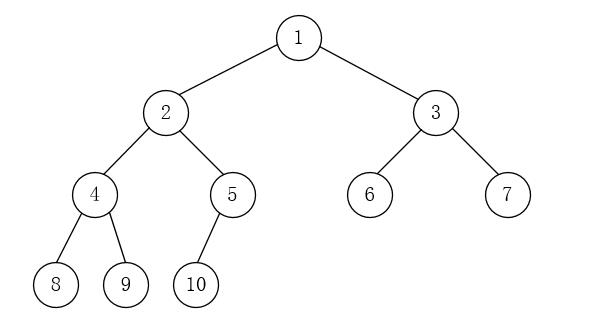
图2-3 完全二叉树

完全二叉树有以下特点：

叶子节点只能出现在最下一层
最下层叶子节点一定集中在左部连续位置。
倒数第二层，如有叶子节点，一定出现在右部连续位置。
同样节点树的二叉树，完全二叉树的深度最小。

二叉树的性质

在二叉树的第i层上最多有 $ 2^{(i-1)} $ 个节点（i >= 1）。
高度为k的二叉树，最多有 $ 2^k-1 $ 个节点 (k >= 0)。
对任何一棵二叉树，如果其叶节点有n个，度为2的非叶子节点有m个，则n = m + 1。（该性质的证明见附录）
具有n个节点的完全二叉树的高度为 $ [log_2n] + 1 $

存储结构

由于二叉树每个节点最多只有两个子节点，因此通常每个节点中有两个指向子节点的指针，如图3-1所示：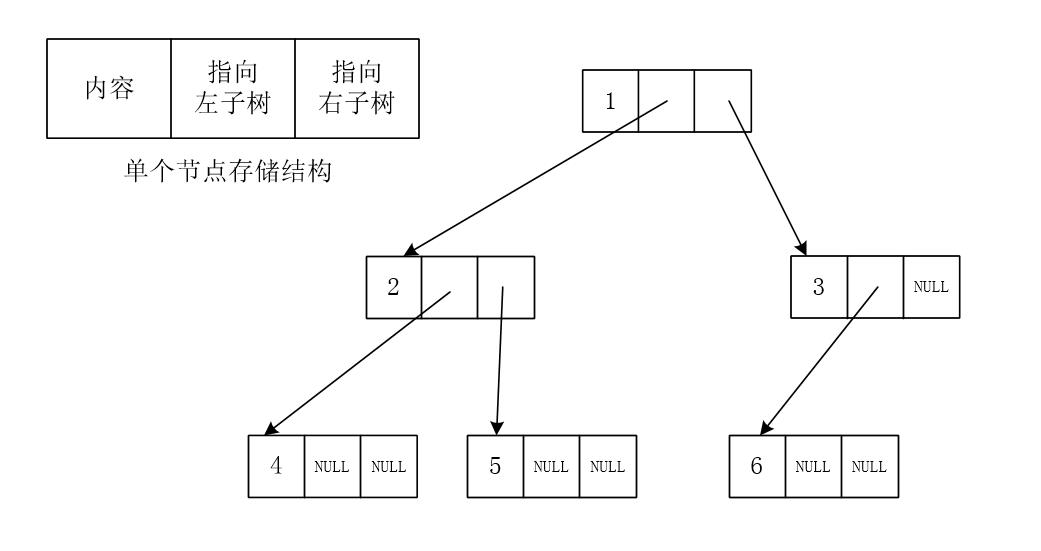
图3-1 二叉树的存储结构
有时为了回溯父节点方便，还会在节点中增加一个指向父节点的指针。

java代码：

class Node {
    Integer val;
    Node left;
    Node right;
    Node parent;

    public Node() { }

    public Node(Integer val, Node left, Node right, Node parent) {
        this.val = val;
        this.left = left;
        this.right = right;
        this.parent = parent;
    }

    public Integer getVal() { return val; }

    public void setVal(Integer val) { his.val = val; }

    public Node getLeft() { return left; }

    public void setLeft(Node left) { this.left = left; }

    public Node getRight() { return right; }

    public void setRight(Node right) { this.right = right; }

    public Node getParent() { return parent; }

    public void setParent(Node parent) { this.parent = parent; }
}

操作

对于一棵二叉树而言，主要有遍历、查找、插入、删除、查询树的高度、树的节点数量以及某个节点的层次等操作。

我们知道二叉树中的每个节点又包含了两棵子二叉树，这本身就是一种递归思想的体现，因此对二叉树的大部分操作使用递归的思想都可以很方便的实现。

广度优先遍历

广度优先遍历实际就是按层次遍历，按节点层次从低到高的顺序遍历所有节点。

比如图2-3中的二叉树的广度优先遍历为：
1 2 3 4 5 6 7 8 9 10

广度优先遍历似乎不太好用递归实现。

广度优先遍历需要使用队列：
（1）首先向队列中插入二叉树的根节点
（2）检查队列中是否有元素，如果队列中没有元素，遍历结束，如果有元素，进行下一步
（3）将队列中的第一个节点弹出，遍历该节点
（4）检查弹出的节点是否有左右子节点，若有，将其插入队列中
（5）重复步骤（2）

该遍历方法运用了队列“先进先出”的特性，先插入的节点也先弹出被遍历。

/** @brief 广度优先遍历 */
public void breadthFisrtTraverse(Node node) {
    LinkedList<Node> queue = new LinkedList<Node>();

    queue.add(node);
    while (queue.size() > 0) {
        Node n = queue.removeFirst();
        System.out.print(n.val + " ");

        if (n.left != null)
            queue.addLast(n.left);
        if (n.right != null)
            queue.addLast(n.right);
    }
}

深度优先遍历

深度优先遍历是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。

深度优先遍历根据遍历时根节点的位置又分为前序、中序和后续遍历。

前序遍历

前序遍历是指按照“根->左->右”的顺序，深度遍历二叉树。

比如图2-3中的二叉树的前序遍历为：
1 2 4 8 9 5 10 3 6 7

/** @brief 前序遍历 */
public void preOrder(Node node) {
    if (node == null)   return;

    // 打印本节点内容
    System.out.print(node.val + " ");
    // 打印左子树
    preOrder(node.left);
    // 打印右子树
    preOrder(node.right);
}

中序遍历

中序遍历是指按照“左->根->右”的顺序，深度遍历二叉树。

比如图2-3中的二叉树的中序遍历为：
8 4 9 2 10 5 1 6 3 7

/** @brief 中序遍历 */
public void midOrder(Node node) {
    if (node == null)   return;

    // 打印左子树
    midOrder(node.left);
    // 打印本节点内容
    System.out.print(node.val + " ");
    // 打印右子树
    midOrder(node.right);
}

后序遍历

前序遍历是指按照“左->右->根”的顺序，深度遍历二叉树。

比如图2-3中的二叉树的后序遍历为：
8 9 4 10 5 2 6 7 3 1

/** @brief 后序遍历 */
public void postOrder(Node node) {
    if (node == null)   return;

    // 打印左子树
    postOrder(node.left);
    // 打印右子树
    postOrder(node.right);
    // 打印本节点内容
    System.out.print(node.val + " ");
}

查找、插入和删除

节点的查找、插入和删除其实都和树的节点顺序有关，比如常用的二叉排序树(BST)中，左节点<根<右节点。因此相关内容将在二叉排序树中再细讲。

查询树的高度

/** @brief 查询以该节点为根的树的高度 */
public Integer height(Node node) {
    if (node == null) return 0;

    return 1 + Math.max(height(node.left), height(node.right));
}

查询树的节点数量

/** @brief 查询以该节点为根的树的节点数量 */
public Integer nodesNum(Node node) {
    if (node == null) return 0;

    return 1 + nodesNum(node.right) + nodesNum(node.left);
}

查询节点的层次

/** @brief 查询节点的层级 */
public Integer level(Node node) {
    if (node == root) return 1;

    return level(node.parent) + 1;
}

附录

性质3的证明

试证明: 对任何一棵二叉树，如果其叶节点有n个，度为2的非叶子节点有m个，则n = m + 1。
证：设一棵二叉树度为0的节点个数为 $ n_0 $, 度为1的节点个数为 $ n_1 $, 度为2的节点个数为 $ n_2 $, 二叉树的节点总数为 k 。
则：
$ k=0 \times n_0+1 \times n_1+2 \times n_2 + 1 $ —— (式 1)
$ k=n_0+n_1+n_2 $ —— (式 2)
两式相减可得：
$ n_0=n_2+1 $ —— (式 3)

由题可知：叶子节点即度为0的节点，即：$ n_0 = n $;
度为2的非叶子节点即度为2的节点，即：$ n_2 = m $;

代入式3可得：
$ n=m+1 $