前言
今天说说树。下面这就是一棵树:
介绍
树是8种基础数据结构(数组Array、栈Stack、队列Queue、链表LinkedList、树Tree、图Graph、堆Heap、散列表HashTable)之一。
一棵树通常可以表示为图2-1的形式,由于其形似一棵倒置的树,它也因此而得名。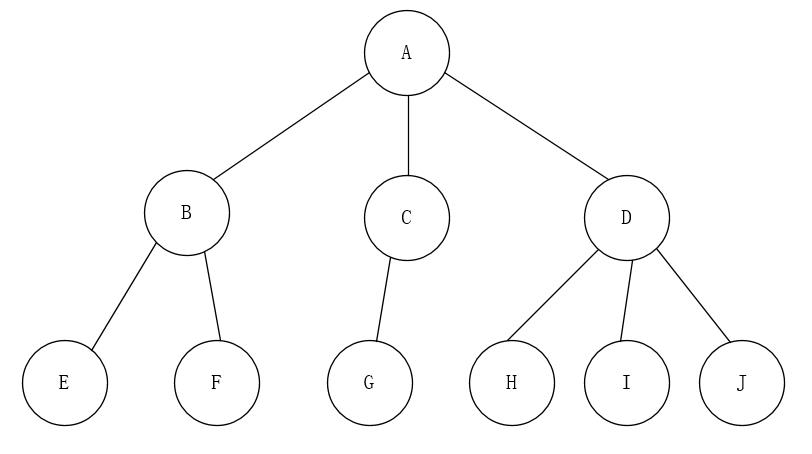
定义
树(Tree)是包含n(n >= 0)个节点的有穷集合。
当 n=0 时,称为 空树。
对于任一棵 非空树(n > 0),其满足以下特性:
- 树中的每个元素称之为 节点(node)
- 有一个特殊的节点称之为 根节点(root),根节点没有父节点
- 除根节点之外的其余数据元素被分为m(m>=0)个互不相交的集合T1,T2,……,Tm-1,其中每一个集合Ti(1<=i<=m)本身也是一棵树,被称作原树的 子树(subtree)
根据上述定义,可以判断图2-2中的均不是树
我们也可以推导出树的一些性质:
- 子树是不相交的
- 除了根节点没有父节点,其余每个节点有且只有一个父节点
- 一棵有n个节点的树,有n-1条边
意义
在笔者看来,树这种数据结构之所以存在有两方面原因:
- 自然界中本来就存在着许多以树状结构存在的事物(比如公司或部门的组织架构,家族图谱等),而程序是对自然界事物的抽象,那么树这种数据结构的出现就非常自然了;
- 在一些大数据量的场景下,树这种数据结构的搜索、插入、删除的综合性能相较与数组、链表有优势。
相关术语
- 节点的度(Degree):一个节点含有的子树的个数称为该节点的度;
- 叶子节点(Leaf):度为0的节点称为叶节点;
- 非终端节点或分支节点:度不为0的节点;
- 父节点(Parent):若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 子节点(Child):一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点(Sibling):具有相同父节点的节点互称为兄弟节点;
- 树的度:一棵树中,最大的节点的度称为树的度;
- 节点的层次(Level):从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度(Depth):树中节点的最大层次;
- 祖先(Ancestor):从根到该节点所经分支上的所有节点都称为该节点的祖先;
- 子孙(Descendant):以某节点为根的子树中任一节点都称为该节点的子孙。
存储模型
由于树的子节点的数量是不确定的,因此通常在节点内部使用链表在存储该节点的子节点,这种表示方法也被称为孩子兄弟表示法,即:
- 每个节点都有一个指向其第一个孩子的指针;
- 每个节点都有一个指向其第一个右兄弟的指针。
图2-1中的树的存储结构可以表示为图3-1所示: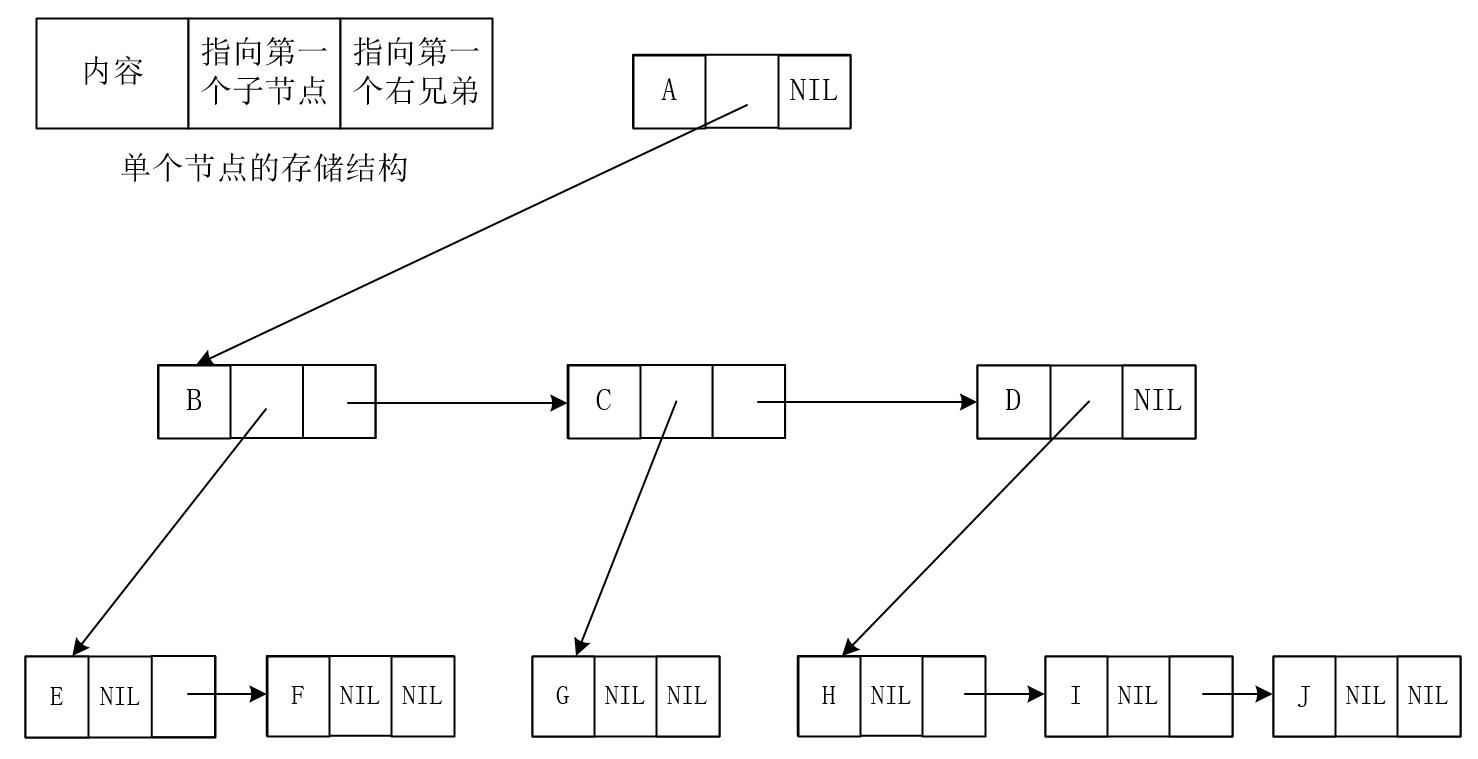
分类及应用
根据是否有序分类
- 无序树
树的任意节点的子节点没有顺序关系。 - 有序树
树的任意节点的子节点有顺序关系。
二叉树
二叉树是应用非常广泛的一种树。
二叉树是指:树的任意节点至多包含两棵子树。
- 满二叉树
叶子节点都在同一层并且除叶子节点外的所有节点都有两个子节点。 - 完全二叉树
对于一颗二叉树,假设其深度为d(d>1)。除第d层外的所有节点构成满二叉树,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树。 - 平衡二叉树
它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,同时,平衡二叉树必定是二叉搜索树。
常用的树
- 二叉查找树(又称二叉搜索树、二叉排序树、BST)
若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
任意节点的左、右子树也分别为二叉查找树;
没有键值相等的节点。 - 红黑树
红黑树是一颗特殊的二叉查找树,它有自平衡的特性,主要用于解决二叉查找树在某些情况下退化为链表而导致性能下降的问题。 - 字典树
又称单词查找树,Trie树,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。 - 后缀树
后缀树(Suffix tree)就是包含一则字符串所有后缀的压缩Trie树。 - 霍夫曼树
带权路径最短的二叉树称为哈夫曼树或最优二叉树。 - 2-3树、B树、B+树、B*树
均为平衡查找树。